Le VIM
Le VIM intitulé JCGM200 par le BIPM est basé sur des concepts de la modélisation de mesure.
Conformément au GUM et au VIM, un résultat de mesure est généralement exprimé par deux valeurs: une valeur mesurée et son incertitude type associée.
La valeur mesurée et son incertitude-type représentent une plage de valeurs comme étant attribuées au mesurande.
Supposons que [x1, u(x1)], ..., [xn, u(xn)] sont les résultats de n mesures différentes pour un mesurande considéré comme suffisamment stable, où x1, ..., xn sont les valeurs mesurées et u(x1), ..., u(xn) sont les incertitudes-types correspondantes.
Dans le concept d'incertitude du GUM, une valeur mesurée xi et son incertitude type associée u(xi) sont considérés respectivement comme la valeur probable (l'espérance mathématique: E(Xi)) et l'écart-type de la densité de probabilité de la fonction dont la connaissance n'est pas complètement déterminée et attribué au mesurande pour i = 1, ..., n.
Le VIM
Le VIM présente un concept de compatibilité métrologique qui ne s'applique qu'aux résultats de la mesure qui sont métrologiquement comparables.
Une valeur mesurée doit être attribuable à une référence métrologique reconnue.
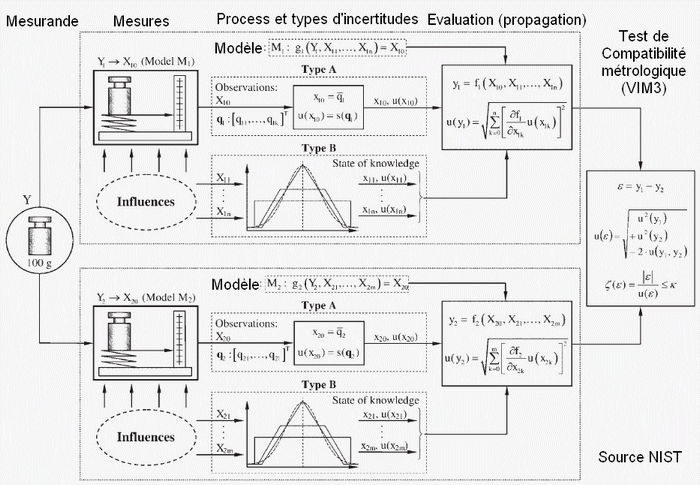
Nous supposons que tous les résultats [x1, u(x1)], ..., [xn, u(xn)] pour un mesurande commun sont traçables à la même référence métrologique et, par conséquent, ils sont métrologiquement comparables.
La valeur mesurée xi est considérée comme la valeur attendue E(Xi) et son l'incertitude type u(xi) est considéré comme l'écart type S(Xi) de la densité de probabilité de la fonction de Xi pour i = 1, 2, j,..., n.
La différence X1 - Xj est une variable issue de la différence entre les valeurs attribuées par les deux résultats [x1, u(x1)] et [xj, u(xj) ] au mesurande commun.
La valeur attendue et l'écart type de la densité de probabilité de la fonction (X1 - Xj) sont, respectivement, E(X1 - Xj) = X1 - Xj et S(X1 - Xj) = √[u²(x1) + u²(xj) - 2r(x1, xj) u(x1) u(xj)], où r (x1, xj) est le coefficient de corrélation entre X1 et Xj.
Selon le VIM, deux résultats métrologiquement comparables [x1, u(x1)] et [xj, u(xj)] pour un mesurande, censé être stable, sont métrologiquement compatibles si | x1 - xj | = k × u(x1 - xj), K: facteur d'élargissement généralement pris égale à 2.
Avec u(x1 - Xj) = √[u²(x1) + u²(xj) - 2r(x1, xj) u(x1) u(xj)]
r(x1, xj) représente le facteur de corrélation entre les données, si r tend vers 1 ou -1, les donnés sont très corrélées, si r=0, les données ne sont pas corrélées.
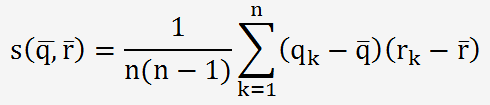 pour
estimer la covariance entre X1=q et Xj=r
pour
estimer la covariance entre X1=q et Xj=r
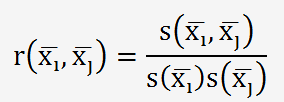 pour
calculer le coefficient de correlation
pour
calculer le coefficient de correlation
Supposons n mesures qui donnent des résultats comparables [x1, u(x1)], [xj, u(xj)], ..., [xn, u(xn)], d'un même mesurande mesuré avec une référence certifiée R, ce qui donne le résultat de référence [xR, u(xR)], où xR est la valeur de référence avec une incertitude type u(xR).
On comprend aisément que pour tracer une courbe d'étalonnage et calculer l'incertitude de la relation Y = F(X) en tout point et avec des fonctions autre que linéaires (polynômes de degré 2, 3 ou 4), soit on se contentera d'une pseudo droite Y= ax+b et il est fort probable que notre valeur ne soit pas fiable et peu réaliste soit on utilisera une méthode plus puissante avec un algorithme approprié : simulation de Monté-Carlo (MCS).
Elle va nous permettre de simuler un très grand nombre de valeurs (1 000 000) autour d'un point, cela pour chaque point et construire autant de courbes: Y1 = F(X1), .....Yn= F(Xn).
Il faudra bien entendu modéliser la relation Y = F(X).
Les équations étant elles-mêmes entachées d'une erreur, on appelle ε (résidu) la différence entre Y1 et Yn.
![]()
Application numérique:
Reprenons l'exemple graphique de la fiche technique: Pente et incertitude d'une tendance linéaire sur un graphique
On titrait une solution inconnue avec un réactif et on relevait les valeurs en mV.
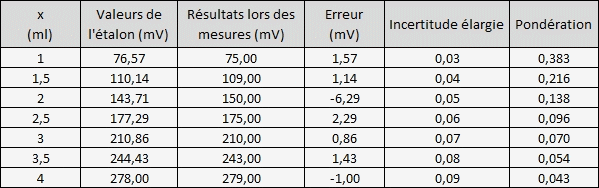
Supposons que cette fois-ci, nous possédons des solutions étalons qui contiennent déjà le volume de titrant et que pour chaque solution est indiquée le potentiel théorique en mV associé à une incertitude élargie.
Dans ce cas précis, il n'y a plus de titrage mais un étalonnage du Titrimètre par simples mesures à différentes concentrations.
L'incertitude des solutions suit une loi normale (k =2), l'erreur de la mesure suit une loi rectangulaire (± 2% de la valeur lue)
La pondération représente l'importance d'une incertitude U1 vis à vis des autres U2, U3, ..,Un.
Elle se calcule par la formule: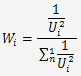
Le choix du degré du polynôme peut être préalablement testé sous excel (des ordres supérieurs à 2 ou à 3 forcent la courbe à passer par plus de points) et elle n'est plus représentative entre les points.
La simulation de Monté-Carlo est réalisée est effectuée avec un logiciel qui génère les coefficients du polynôme (choix du degré 2).
| i |
a |
u(a) |
| 0 |
7,387 |
3,782 |
| 1 |
0,902 |
0,0573 |
| 2 |
0,000277 |
0,000184 |
Les valeurs ont été volontairement arrondies.
| r |
a0 |
a1 |
a2 |
| a0 |
1 |
-0,977 |
0,935 |
| a1 |
-0,977 |
1 |
-0,983 |
| a2 |
0,935 |
-0,983 |
1 |
On voit que les coefficient sont très corrélés.
Le résidu moyen estimé par la méthode
de Monte Carlo vaut : ε = -0,102.
L'incertitude type sur cette valeur est : u(ε) = 3,227.
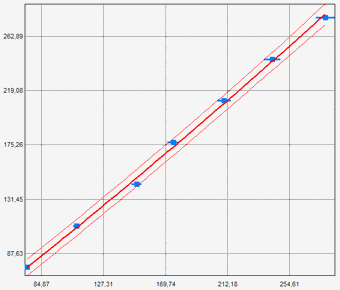
Pour une lecture de 150 mV avec une erreur associée de ±2%, alors la valeur Y = 148,9 mV avec U = ±4,5 mV avec K = 2
